[论文阅读] Attention is All you Need
encoder将符号表示的输入序列\((x_1,\dots,x_n)\)映射到连续表示的序列\((z_1,\dots,z_n)\)。给定\(z\),decoder再逐元素生成输出的符号序列\((y_1,\dots,y_n)\)。
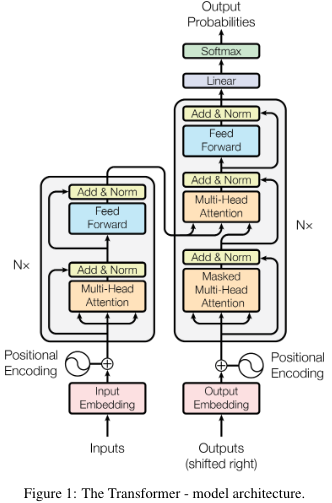
Encoder
encoder是由6个相同的层堆叠而成的,每层又包含2个字层,第一层是多头注意力机制,第二层是简单的全连接前馈网络。两个子层之间使用残差连接,然后进行归一化,即每个子层的输出为\({\rm LayerNorm}(x + {\rm Sublayer}(x))\)。为了便于实现残差连接,所有输出的维数均为\(d_{model}=512\)
Decoder
decoder也是由6个相同的层堆叠而成的,除了先前提到的两个子层外,decoder还添加了第三个子层,对encoder的输出进行多头注意力。跟encoder相似,decoder在每个子层间也添加了残差连接,然后进行归一化。此外,decoder中的自注意力添加了mask机制,确保对于位置\(i\)的预测是依赖小于\(i\)的已知位置输出得到的。
Attention
attention函数可以理解为将一个查询和一组键值映射到一个输出上。
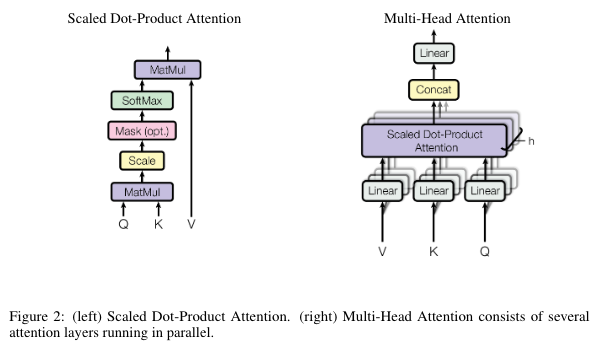
Scaled Dot-Product Attention
\[ {\rm Attention}(Q,K,V)={\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V \]
Multi-Head Attention
与单一的注意力函数统一投影到\(d_{model}\)维不同,将查询、键值分别投影到\(d_k,d_k,d_v\)维有收益。在查询、键值的这些映射版本上并行执行注意力机制,生成\(d_v\)维的输出,最终连接起来再次映射,得到最终输出。
\({\rm MultiHead}(Q, K, V)={\rm Concat(head_1,\dots,head_h)}W^O \\ {\rm where\ head_i=Attention}(QW_i^Q,KW_i^K,VW_i^V)\)
\(W_i^Q\in\mathbb{R}^{d_{model}\times d_k}, W_i^K\in\mathbb{R}^{d_{model}\times d_k}, W_i^V\in\mathbb{R}^{d_{model}\times d_v},W^O\in\mathbb{R}^{hd_v\times d_{model}}\)
\(h=8,d_k=d_v=d_{model}/h=64\)
Position-wise Feed-Forward Networks
除了注意力子层外,encoder和decoder的每一层都包含一个全连接的前馈网络,分别作用于每个位置。两个线性变化中包含一个ReLU激活函数。 \[ {\rm FFN}(x)=\max(0, xW_1+b_1)W_2+b_2 \]
虽然线性变换在不同位置上是相同的,但是他们使用的是不同的参数。
Embeddings and Softmax
在两个embedding层和pre-softmax线性变换之间共享相同的权重矩阵。在embedding层中,将权重乘以\(\sqrt{d_{model}}\)
Position Encoding
由于模型不包含递归和卷积,为了使模型能够利用序列中的顺序信息,必须在序列中注入一些关于token相对或绝对位置的信息。为此,在encoder和decoder堆栈的底部将位置编码加到了输入中,位置编码的维度与input embedding的相同,均为\(d_{model}\),方便相加作为新的输入。计算位置编码的方式有很多,包括可学习的和固定的。
本文中,对不同的序列选择正弦和余弦函数来计算:
\(PE_{(pos,2i)}=\sin(pos/10000^{2i/d_{model}})\)
\(PE_{(pos,2i+1)}=\cos(pos/10000^{2i/d_{model}})\)
其中\(pos\)是位置索引,\(i\)是维数索引。位置编码的每个维度对应一条正弦曲线。波长呈\(2\pi\)到\(100000\cdot2\pi\)的几何级数。之所以选择这样的函数是因为:
- 可以直接计算embedding不需要训练,减少了训练参数
- 允许模型将position embedding扩展到比训练过程中遇到的序列长度更长的序列